Why Music Sounds Musical

I wrote a piece called "Some Musical Theory, from a Christian Perspective" that discussed some of the mathematical aspects of musical theory, and I related that theory to some of the physics of how musical sound is made and how our ears and brains are constructed to hear it. It demonstrates how God designed us to recognize and appreciate music. Much of this I learned from a wonderful book called The Science of Musical Sound by John R. Pierce.

I regret that the wonderful message of that piece is not accessible to those that are not inclined to mathematics. I sympathize with them because in my career as an engineer, I have sometimes been 'dragged kicking and screaming' as I often have said, into the intricacies of mathematics because it was necessary to get my work done.

So here I will try to extract the basic ideas of that piece, leaving behind the equations and as much math as I can, and present them in a more palatable form. Here goes ..

Making Musical Sound

Music is made by vibrations: sometimes the shaking of strings, or sometimes of surfaces, but always involving the shaking of air, because sound is a moving variation of air pressure. The notes with higher pitch involve faster shaking, so that we can measure the pitch by measuring the number of shakes per second, called the frequency.

A string pulled tightly between two anchor-points can vibrate, as in many musical instruments. The frequency (pitch) will increase with increased tension, or with less weight of the string. or with decreased length between the anchor-points. (The bass strings of a piano are wrapped with heavy wire to save making the piano larger.) For the same weight and tension, a string half as long will have twice the frequency.

Air vibrates inside a long tube or pipe in other instruments. A pipe half as long will have twice the frequency, as for the strings.

When a string is plucked or struck or bowed near one end, the energy given to the string travels down the length of the string and bounces back and forth between the two anchor-points. When the air in a tube or pipe is made to vibrate by blowing over a hole or by a vibrating reed near one end, the energy given to the air travels down the length of the tube and bounces back and forth between the two ends of the tube. So in the case of a longer string or a pipe, the energy must travel further, so the vibration is slowed down, making a lower frequency.

Modes of Vibration

In its simplest mode of vibration, a string bends back and forth between two positions represented by the solid and dotted lines in the next diagram:
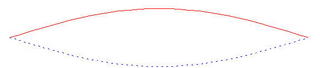But the string can also bend back and forth between these two positions:
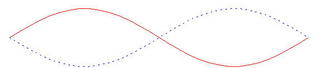... Or bend back and forth between these two positions:
... And so forth.

The same modes occur in the case of air vibrating in a pipe. The first mode is called the fundamental, and the others are called overtones. The first overtone, where the string vibrates in two sections, has twice the frequency of the fundamental. The second overtone has three times the frequency, etc.

An example (for musicians): If the fundamental were middle C, the first overtone is C one octave higher (twice the frequency). The second overtone is the G a fifth interval higher (3/2 the frequency) than the first overtone. The third overtone is the next C a fourth interval higher (4/3 the frequency) than the second overtone. Notice that we get a lot of frequency ratios: 2/1, 3/2, 4/3, etc.

In most cases, especially when the string is plucked, struck, or bowed near the end of the string, the string actually vibrates in all these modes at the same time. That is, the actual motion is the sum of all these simple motions, with the overtones generally weaker as they go higher.

Hearing Tones

If the tones of the fundamental and overtones were sounded by separate strings, our ears would hear a chord (a set of related notes), but when these tones come from a single vibrating string, we hear one note with a rich sound that is more interesting than hearing only the fundamental. Another way of describing it is that we hear one note having the fundamental tone, but enriched by the overtones.

We hear the chord because the separate strings normally are not perfectly tuned, and we can hear that the frequency ratios are not exact. We hear the single rich-sounding note because the tones are 'locked' by perfect ratios, and our ears can hear the difference. How can our ears do this?

Sound entering one of our ears shakes our ear-drum, which shakes the three tiniest bones in our body (all three fit on a dime), which act as an adjustable lever, or volume control. These tiny bones transfer the sound vibrations to the cochlea, a snail-shaped organ in the inner ear. The cochlea is a coiled and tapered tube, with the fattest end connected to the bones.

If the tube of the cochlea were sliced, it would look like the diagram on the left, which shows the interior of the tube divided into three regions (shown as gray) filled with fluid: the vestibular canal (top) , the tympanic canal (bottom), and the cochlear duct (middle). The inner-most bone (the stapes) is attached to the oval window at the fat end of the vestibular canal. The sound pressure travels down the vestibular canal to the small end of the cochlea, where it connects to the tympanic canal. Then the sound pressure travels back up the tympanic canal to the fat end of the cochlea, ending at the round window below the oval window.

The pressure wave travelling down the top side reacts with the pressure wave travelling up the bottom side through the vestibular membrane and basilar membrane that separate them. The result is that high frequency tones shake the basilar membrane near the fat end of the cochlea, and low frequency tones shake the basilar membrane near the small end. Hair cells connected to nerve fibers leading to the brain detect the vibration of the basilar membrane. When we are hearing a complex sound with many frequencies, we hear each frequency component at a different place along the length of the cochlea. The precision of this detection is so good that scientists are baffled to fully explain it.

Hearing Chords

Another question that needs to be answered is: Why do the combinations of notes that we call chords appeal to us as sounding 'musical'? The key to the answer is the overtones that we described earlier. Take for example, the C major 7th chord CEGB. In the chart below, we list the positions of the fundamental tones (1) and overtones (2,3,4..) of each note of the chord (row labels at left) in the musical scale (column labels at top) :
The letters X, Y, Z, etc. on the bottom of the chart mark positions where overtones of different notes of the chord nearly match in frequency. Because the notes are never perfectly tuned, the overtones match, but not perfectly, and the small difference causes an interaction called the 'beat' effect that signals our ears that these notes are 'connected' to each other. Because the lower overtones are generally louder, this kind of 'connection' is stronger for pairs of notes related by a frequency ratio that is expressed by smaller integers -- what we call 'simple ratios'.

For musicians: The fact that our musical sensibilities favor simple frequency ratios leads to the spacing of the notes in a major scale, and is the basis of chord structure and melody. Using just a few mathematical rules about these simple ratios, the frequency of all the notes of any scale, and the sharps and flats for all of the keys can be calculated.

Summary

When we examine in detail how our hearing is designed, we can see that its capabilities goes beyond what is needed for recognition and interpretation of speech -- it has 'bonus' features designed for the appreciation of music.