Tuesday, May 22, 2007
The Better Mouse Trap
We sometimes had mice (I remember Mom catching one with a broom and a dustpan), so we also had mousetraps. I noticed that mice could sometimes nibble the cheese gently enough to avoid getting caught, so I concluded that the triggering lever wasn’t sensitive enough. The big strong lever for catching the mouse was held by a second lever, which in turn was held by a third triggering lever that held the cheese.
I figured out that the purpose of the second lever was to reduce the force at the triggering lever. But the problem was that the triggering force was not reduced enough. So I built a mouse trap with more levers. As best as I can recall, the improved design was something like this:
A triggering lever made of a length of horse-hair held a stouter lever made of a broom-straw, which held a lever made of a tooth-pick, which held a lever made of a Popsicle stick, which held the strong capturing lever. The horse-hair didn’t need to hold the cheese, because the mouse’s whiskers would spring the trap if he just got close enough to sniff the cheese.
To test the trap, I set it up on the stairs that went from the kitchen up to the boys’ bedroom. (My three brothers and I shared one big bedroom.)
Now you must understand that one could not tip-toe up these stairs without most of the steps creaking. (This was advantageous to us boys when our parents could hear mischievous noise coming from the bedroom, and one of them tried to sneak up the stairs to find out who was doing what. But that’s another story.) But actually you could sneak up the stairs noiselessly if you knew the secret sequence: step over the first three steps, landing on the far left side of the fourth step, then go to the far right of the sixth step. etc.
Because the trap was essentially a vibration sensor, I thought that by setting it up near the top of the stairs, one of my brothers would walk up the stairs, would creak a step near the trap, and then be surprised by the trap snapping.
So I set up the mouse trap on the stairs – easy to say, but tedious to do. First, pull back the big spring lever, then get the Popsicle stick to hold it down, then set the tooth-pick to hold the Popsicle stick, then set the broom-straw to hold the tooth-pick, then set the horse-hair to hold the broom-straw. The process got more and more delicate.
That done, I next had to retreat, navigating the secret sequence in reverse. I tip-toed down nearly to the bottom when I miscalculated, a step creaked, and ten steps above me, the trap snapped shut.
That was the end of the experiment. I concluded that the trap was a bit too sensitive.
Sunday, May 20, 2007
The Nine-Bite Sandwich
The Nine-Bite Sandwich is a Construction process followed by an Eating process, which I will explain with patent-style drawings. Since it is not patented, I hereby put it into the Public Domain.
Ingredients
The ingredients are two slices of bread and four different spreads of your choice. For the bread, use sandwich bread — the real kind, not that so-called 'Wonder bread' ("I wonder why they call it bread", I always say) that sticks to your gums and palate. For the spreads, I will illustrate with peanut butter (PB), margarine (M), blueberry jam (BB) and strawberry preserves (SB); but you can choose your own.
The Construction Process
As shown in Figure 1, lay the slices of bread (S1 and S2) down in a symmetrical position. This is needed so that the slices will fit neatly when one slice is turned over onto the other slice.
Figure 1

As shown in Figure 2, spread margarine (M) on the left half of slice S1, and spread peanut butter (PB) on the right half of slice S1. Also, spread blueberry jam (BB) on the top half of slice S2, and spread strawberry preserves (SB) on the bottom half of slice S2.
Figure 2

As shown in Figure 3, turn slice S1 (the one on the left) onto slice S2. Notice that this instantly creates four flavor combinations as shown.
As shown in Figure 4, take the first four bites from the corners of the sandwich as shown. You can peek first, to anticipate each flavor combination, or you can surprise yourself by flipping or rotating the sandwich a few times first.

As shown in Figure 5, take the next four bites from the 'arms' of the cross shape left by the first four bites. Notice that these bites are three-flavor combinations — a more complex flavor experience.
Figure 5 
The remaining center is the last, ninth bite. It combines the flavors of all four spreads. This sandwich is fun to make and eat because each bite is a different flavor combination. Yet the sandwich is really quite easy to make.
Wednesday, January 31, 2007
Susan's Novel to be Published Soon

I haven't been posting for a while, because my computer died, and I lost my Internet connection. Now I'm back.
The big news around here is that my daughter Susan has found a publisher (Publish America) for her novel (And the Violin Cried). It will be published by late February or March. You can read reviews and articles about it, and get up-to-date news about book signings, etc. at www.PublishedAuthors.net/SusanJoyClark.
I've transitioned from being her nit-picking editor to being her Publish America Publicity Agent (PA PA). (ha ha) So I set up and maintain web sites, design and print business cards and bookmarks for her. I have also done photography for her, including photos of three young friends who posed as three of the characters in the novel.
Susan, who has training in graphic design, has designed a book cover for her novel which uses these three photos. The publisher may use her cover design as is, or may modify it, or do something different (no promises). But when we saw the page proofs, we were happy to see that the photos were incorporated into the book. Various chapters tell the story from the point of view of different characters; and each photo appears at the beginning of the chapter that first takes that character's point of view. We are taking that as a sign that the publisher likes Susan's cover design as well.
We decided that the title page should feature a picture of a violin, so we found a violin shop and asked if we could take a photo of a violin. They were quite gracious in spite of the fact that they were quite busy. One wall was covered with hundreds of violins. We explained that her novel featured a Schweitzer violin that survived the Holocaust, and the lady took a violin from the wall, and handing it to me, said "This one's a Schweitzer."
"Really?", I said, and she explained that it was actually a replica. But the way it was finished, it looked like an old violin that was re-varnished.

Wednesday, August 03, 2005
Dawkins' Weasel Algorithm, Revisited
Each character position (or column in the list of states) of the "Weasel" Algorithm can be described as an independent Markov process.
A Markov process has a set of states, and there are fixed probabilities for all possible transitions from one state to another. Take, for example, the process of tossing a die until it comes up "5".
 The diagram at left describes this as a Markov process. The states are represented by the numbered circles. The interconnecting lines with arrow-heads represent one-way transitions from one state to the next. Lines without arrow-heads represent a pair of transitions in opposite transitions. Note that the looping arrow-lines indicate that a state may sometimes transition to itself -- for example, when the die is "1" and on the next toss is "1" again. Generally, probability values are written next to the transition lines in a Markov graph, but here we will simply state that all the transitions that exit any state are equally probable.
The diagram at left describes this as a Markov process. The states are represented by the numbered circles. The interconnecting lines with arrow-heads represent one-way transitions from one state to the next. Lines without arrow-heads represent a pair of transitions in opposite transitions. Note that the looping arrow-lines indicate that a state may sometimes transition to itself -- for example, when the die is "1" and on the next toss is "1" again. Generally, probability values are written next to the transition lines in a Markov graph, but here we will simply state that all the transitions that exit any state are equally probable.In this case, state "5" has no exits except the transition to itself because we stop tossing the die when it comes up "5". This called an absorbing state.
Markov processes can be analyzed by means of matrix algebra and graph theory, and in the case (as here) where there is one absorbing state which is reachable (there is a path to it) from all other states, it can be proved that the process will always end in that state.
Let us return to our statement that each character position of the "Weasel" Algorithm can be described as an independent Markov process. Each of these Markov processes are similar in form to the one that we illustrated in the above transition graph, except that it has 53 states instead of 6. And the template (the target phrase) determines, for each character position (each independent Markov process) which state will be the absorbing state. So, as we said earlier, the mathematics of Markov processes can be used to prove that each independent Markov process will stop in its absorbing state. Since the template determines the absorbing states, it also determines the results before the independent processes even start.
Let us return for a moment to the process of tossing a die until it comes up "5". It should be obvious that since we mentioned "5" in the definition of the process, there is no need to do anything random to get the result "5", because "5" is selected before we even start. Likewise for Dawkins' "Weasel" Algorithm, the random events do not select the result, because we selected it when we defined the template, or target phrase.
Thus we have shown that the information of the result of Dawkins' "Weasel" Algorithm does not come from the randomness, but from the definition of the explicit form of the algorithm. That is, the information is present before the process even starts.
It is also easy to show that Dawkins' "Weasel" Algorithm does not come close to approximating an evolutionary process. This is because the processes at each character position are independent. This is equivalent to saying that each bone, each muscle, etc. of an animal evolves independently, which of course is preposterous.
In the future, I will discuss more serious algorithms that seek to simulate or model evolution. However, there will be a delay, because I will shortly be off on a one-week trip, and when I return, my computer will be off for some serious repair. (Right now, it doesn't do much more than a WebTV.)
Tuesday, August 02, 2005
Why Music Sounds Musical
I regret that the wonderful message of that piece is not accessible to those that are not inclined to mathematics. I sympathize with them because in my career as an engineer, I have sometimes been 'dragged kicking and screaming' as I often have said, into the intricacies of mathematics because it was necessary to get my work done.
So here I will try to extract the basic ideas of that piece, leaving behind the equations and as much math as I can, and present them in a more palatable form. Here goes ..
Making Musical Sound
Music is made by vibrations: sometimes the shaking of strings, or sometimes of surfaces, but always involving the shaking of air, because sound is a moving variation of air pressure. The notes with higher pitch involve faster shaking, so that we can measure the pitch by measuring the number of shakes per second, called the frequency.
A string pulled tightly between two anchor-points can vibrate, as in many musical instruments. The frequency (pitch) will increase with increased tension, or with less weight of the string. or with decreased length between the anchor-points. (The bass strings of a piano are wrapped with heavy wire to save making the piano larger.) For the same weight and tension, a string half as long will have twice the frequency.
Air vibrates inside a long tube or pipe in other instruments. A pipe half as long will have twice the frequency, as for the strings.
When a string is plucked or struck or bowed near one end, the energy given to the string travels down the length of the string and bounces back and forth between the two anchor-points. When the air in a tube or pipe is made to vibrate by blowing over a hole or by a vibrating reed near one end, the energy given to the air travels down the length of the tube and bounces back and forth between the two ends of the tube. So in the case of a longer string or a pipe, the energy must travel further, so the vibration is slowed down, making a lower frequency.
Modes of Vibration
In its simplest mode of vibration, a string bends back and forth between two positions represented by the solid and dotted lines in the next diagram:
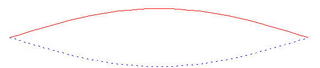 But the string can also bend back and forth between these two positions:
But the string can also bend back and forth between these two positions: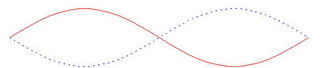 ... Or bend back and forth between these two positions:
... Or bend back and forth between these two positions: ... And so forth.
... And so forth.The same modes occur in the case of air vibrating in a pipe. The first mode is called the fundamental, and the others are called overtones. The first overtone, where the string vibrates in two sections, has twice the frequency of the fundamental. The second overtone has three times the frequency, etc.
An example (for musicians): If the fundamental were middle C, the first overtone is C one octave higher (twice the frequency). The second overtone is the G a fifth interval higher (3/2 the frequency) than the first overtone. The third overtone is the next C a fourth interval higher (4/3 the frequency) than the second overtone. Notice that we get a lot of frequency ratios: 2/1, 3/2, 4/3, etc.
In most cases, especially when the string is plucked, struck, or bowed near the end of the string, the string actually vibrates in all these modes at the same time. That is, the actual motion is the sum of all these simple motions, with the overtones generally weaker as they go higher.
Hearing Tones
If the tones of the fundamental and overtones were sounded by separate strings, our ears would hear a chord (a set of related notes), but when these tones come from a single vibrating string, we hear one note with a rich sound that is more interesting than hearing only the fundamental. Another way of describing it is that we hear one note having the fundamental tone, but enriched by the overtones.
We hear the chord because the separate strings normally are not perfectly tuned, and we can hear that the frequency ratios are not exact. We hear the single rich-sounding note because the tones are 'locked' by perfect ratios, and our ears can hear the difference. How can our ears do this?
Sound entering one of our ears shakes our ear-drum, which shakes the three tiniest bones in our body (all three fit on a dime), which act as an adjustable lever, or volume control. These tiny bones transfer the sound vibrations to the cochlea, a snail-shaped organ in the inner ear. The cochlea is a coiled and tapered tube, with the fattest end connected to the bones.
 If the tube of the cochlea were sliced, it would look like the diagram on the left, which shows the interior of the tube divided into three regions (shown as gray) filled with fluid: the vestibular canal (top) , the tympanic canal (bottom), and the cochlear duct (middle). The inner-most bone (the stapes) is attached to the oval window at the fat end of the vestibular canal. The sound pressure travels down the vestibular canal to the small end of the cochlea, where it connects to the tympanic canal. Then the sound pressure travels back up the tympanic canal to the fat end of the cochlea, ending at the round window below the oval window.
If the tube of the cochlea were sliced, it would look like the diagram on the left, which shows the interior of the tube divided into three regions (shown as gray) filled with fluid: the vestibular canal (top) , the tympanic canal (bottom), and the cochlear duct (middle). The inner-most bone (the stapes) is attached to the oval window at the fat end of the vestibular canal. The sound pressure travels down the vestibular canal to the small end of the cochlea, where it connects to the tympanic canal. Then the sound pressure travels back up the tympanic canal to the fat end of the cochlea, ending at the round window below the oval window.The pressure wave travelling down the top side reacts with the pressure wave travelling up the bottom side through the vestibular membrane and basilar membrane that separate them. The result is that high frequency tones shake the basilar membrane near the fat end of the cochlea, and low frequency tones shake the basilar membrane near the small end. Hair cells connected to nerve fibers leading to the brain detect the vibration of the basilar membrane. When we are hearing a complex sound with many frequencies, we hear each frequency component at a different place along the length of the cochlea. The precision of this detection is so good that scientists are baffled to fully explain it.
Hearing Chords
Another question that needs to be answered is: Why do the combinations of notes that we call chords appeal to us as sounding 'musical'? The key to the answer is the overtones that we described earlier. Take for example, the C major 7th chord CEGB. In the chart below, we list the positions of the fundamental tones (1) and overtones (2,3,4..) of each note of the chord (row labels at left) in the musical scale (column labels at top) :
 The letters X, Y, Z, etc. on the bottom of the chart mark positions where overtones of different notes of the chord nearly match in frequency. Because the notes are never perfectly tuned, the overtones match, but not perfectly, and the small difference causes an interaction called the 'beat' effect that signals our ears that these notes are 'connected' to each other. Because the lower overtones are generally louder, this kind of 'connection' is stronger for pairs of notes related by a frequency ratio that is expressed by smaller integers -- what we call 'simple ratios'.
The letters X, Y, Z, etc. on the bottom of the chart mark positions where overtones of different notes of the chord nearly match in frequency. Because the notes are never perfectly tuned, the overtones match, but not perfectly, and the small difference causes an interaction called the 'beat' effect that signals our ears that these notes are 'connected' to each other. Because the lower overtones are generally louder, this kind of 'connection' is stronger for pairs of notes related by a frequency ratio that is expressed by smaller integers -- what we call 'simple ratios'.For musicians: The fact that our musical sensibilities favor simple frequency ratios leads to the spacing of the notes in a major scale, and is the basis of chord structure and melody. Using just a few mathematical rules about these simple ratios, the frequency of all the notes of any scale, and the sharps and flats for all of the keys can be calculated.
Summary
When we examine in detail how our hearing is designed, we can see that its capabilities goes beyond what is needed for recognition and interpretation of speech -- it has 'bonus' features designed for the appreciation of music.
Monday, August 01, 2005
ALL Things
All things were made through Him, and without Him nothing was made that was made.
John 1:3 (NKJV)
Modern science provides a remarkable perspective and insight to the "all things" of this verse. As summarized by the famous formula E=mc2, energy and mass (matter) are interchangeable; thus the creation must include not only material things (matter), but also all forms of energy.
Also, Einstein's theory of relativity, confirmed by experiments and measurements, shows that time and space are different sides of the same fabric.
More recent physics theories describe matter and energy as wrinkles or knots in the fabric of space-time. Space cannot exist empty, that is, without matter and energy.
So everything is inexorably, inextricably joined. Time cannot pass without space also existing, and space cannot exist empty, without matter and energy. So when "God created the heavens and the earth" (Gen. 1:1), the eternal God created a wondrous unity: matter, energy, space, and time, and all of the 'laws of physics' that make these a cohesive whole.
God must exist apart from time, because time is part of His creation. I used to think that the eternalness of God meant that He was infinitely old; but no, He can exist outside of time. And outside of space, and not made of matter or energy. And because He created all of these, that makes Him older and bigger and more powerful and massive than all that He has created.
Read it again:
All things were made through Him, and without Him nothing was made that was made.
But because of His great love and concern for His creation, He entered His own world and became one of His own creatures, that we might know Him better, and not be strangers to Him. Read verses 10 to 12 that follow soon after the above verse:
He was in the world, and the world was made by Him, and the world knew Him not.
He came unto His own, and His own received Him not.
But as many as received Him, to them gave He power to become the sons of God, even to them that believe on His name.
That name is Jesus -- which means Savior.
NOTE: Another blog considers whether information should be added to the unity of matter, energy, space, and time.
Friday, July 29, 2005
Praying for Strangers
I don't fully understand why I get these occasional quiet urges to pray for a stranger. Sometimes I wonder whether it's a look of worry or concern that I sense in their face, but then I doubt that I get that good a look as I pass by. Maybe it's because I am aware that God is watching over everyone, believers and unbelievers, and cares about them, and wants them to trust Him, so He can guide them. I know He wants to be involved, but doesn't force Himself upon anyone.
But I know that God does answer prayer, even prayers for strangers. Scientists have repeatedly done controlled, randomized, double-blind experiments that time and again have demonstrated the effectiveness of prayer. In most of these experiments, the praying person and the prayed-for person do not know each other.
Even in the face of the scientific evidence, some disbelieve and try to explain it away, which is probably why these kinds of experiments have been done so many times. Professor Leslie Francis of the University of Bangor has studied 31 experiments (conducted to the "highest professional standards") into the effectiveness of prayer. And this research report, although not entirely Biblical, makes some interesting observations and arguments about prayer.
Wednesday, July 27, 2005
Growing Up Shy
I don't remember interacting much with other kids in kindergarten -- I avoided competition for the toys, and preferred to play by myself. But I do remember once talking to another boy. I was playing with some turtle-shaped metal containers on a window sill when the boy told me that he wished that the sunshine would shine on the other side of the room opposite from the windows. I told him that the sun was high in the sky and light travels in straight lines, so it couldn't reach that side of the room. (Many years later, I wondered how I knew at that age that light travels in straight lines, and figured that it might have been from clapping with chalky hands and seeing the sunlight from the window make straight beams in the cloud of dust.)
As I progressed through school, I didn't talk much, so most of the other kids ignored me. But I was watching them. I remember at an early age having an infatuation with a pretty girl that sat about four seats in front of me. One day I left a note in her desk before she arrived in the classroom, saying "I love you. Jimmy". I assumed that she would be as secretive about it as I was, but no -- when she found it, she blurted out loud to the girls around her "Oh, isn't this cute, Jimmy loves me!" I wished there was a trap-door in the floor that I could disappear through. I learned that communication with the opposite sex was hazardous.
Shy people are careful about talking, especially with strangers, because they are not sure what the reaction will be. They prefer to listen and observe, and I think that they learn more. But talking wasn't a problem at home -- I talked and talked -- they said I lectured. They called me "the professor" or sometimes "the absent-minded professor".
In gym class, however, communication was physical, and I felt I could get some respect. When playing dodge ball, most boys figured that the safest strategy was to hide behind someone else. But when the ball was thrown at the boy in front, you couldn't see the ball coming, and didn't have enough time to react to the direction that he dodged. I thought it was safer to stay in the open where you could see the ball coming, and in back where you had more reaction time. So I was often the last one left, and they would gang up on me, throwing two balls at once. I soon learned how to dodge two balls at once. The trickiest situation was when one ball was high and one low -- I jumped up and turned horizontal, putting my body between the two balls.
Another gym activity took place on a wrestling mat. Half a dozen boys started on the mat. Any one touching the floor off the mat would be out of the game, until only one was left. I had experience wrestling with my three brothers, so it was hard to get me off the mat. Again, they ganged up on me. Four boys went after me, each taking one leg or arm. But I could sense which of them had a solid stance on the mat, and which could be more easily pushed or pulled over. So I braced myself against the ones that were solid to push or pull the others. Another part of the strategy was confusing them as to whether it was a pulling struggle or pushing. And, since they surrounded me, I was in the middle, and less likely to be the first one over the edge of the mat. We went at it for quite a while before the instructor finally stopped the game.
When I was in college, an Israeli student, Marvin Haufmann, befriended me. I remember many times when he would be sitting at a table in the school cafeteria with his Israeli buddies, chatting in Hebrew. He would motion me to come join them, and tell his buddies to switch to English for my sake. Several of them had been aircraft mechanics in the Israeli Air Force, and it was interesting to hear their recollections of 24-cylinder aircraft engines, and other stories. But what was more interesting was how they shared stories and concerns without embarrassment, what a shy person would be afraid to discuss, and everyone was quite accepting. I thought I could learn to talk like that, too, and that's when I started to lose my shyness.
Tuesday, July 26, 2005
Communication
In engineering work, there are a lot of specialties -- different people have different areas of expertise. For any project, a variety of specialties are needed, and they need to communicate and cooperate to fulfil all the needs of the project. There were situations where I had longer and broader experience than others on the project, but nonetheless, they had more expertise than I in certain important areas. So I showed respect for their expertise and they showed respect for mine.
Take for example the Phase Meter invention that I mentioned in my post "Invention or Discovery". The performance of the phase meter was predicted by simulations and 'paper' analysis -- no actual phase meter was built. So at some point, my boss asked me to build and test a prototype model, with the help of others. Part of the design was hardware, detailed by two engineers in Ft. Wayne, Indiana. Another part of the design was software, detailed by two programmers in San Diego, California. And I guided them, providing data from my simulations, in Clifton, New Jersey (all ITT locations). I didn't know any of the others beforehand, except John Petzinger (co-inventor), but communicated mostly by email, and occasionally by telephone. I saw some of them face to face when we were finally ready to put it all together and test it. But it was a success, proving the simulations to be correct.
Knowing that people tend to distrust strangers, I showed appreciation for their work at every opportunity, respect and thanks for their ideas, and honest praise (but not overdone. or it wouldn't sound sincere) when they were successful. Then whenever it became necessary for me to criticize or point out errors, it was not taken personally, but accepted as necessary to make the project a success. And I was careful to admit my own errors when that happened, and to thank them for finding them. After a while, I sensed a friendly tone in their e-mails, and sensed that they were not afraid to ask for help when needed, nor embarrassed to admit that they didn't understand something. Such barriers to communication can seriously hurt a project, because full cooperation and complete and accurate knowledge is important when a project is full of many complex details.
On another project, I first made the acquaintance of an engineer by email, and my initial impression was that he was careless or misinformed. However, it turned out that he was quite careful and knowledgable, but awkward expressing himself in writing.
I recall two cases where another engineer did something dumb and had a bad attitude, although most of the time people were intelligent and civil. In the first case, the engineer connected some data paths so that sometimes the data was reversed. It was like making a dictionary where sometimes the words are spelled backwards. ('Provide' is listed near 'edition' because it is spelled 'edivorp'.) When the error was pointed out to him, he insisted that nothing was wrong, and refused to change the connections. Soon afterward, he was fired.
Several years later, I wrote a specification for a digital radio design, and another engineer working miles away decided to ignore the specification. The specified data sequence was not compatible with test equipment that he wanted to use, making it inconvenient for him to test the radio. So he changed the design to fit the test equipment, rather than adapt the test equipment to fit the design. Again, it was improper data reversal, and refusal to correct the design. The design needed to be as specified to be compatible with another radio.
He didn't work directly for me, so I couldn't make him change it. I had to explain the situation to my boss, who talked to his boss, who made him change it. But I still had to work with him (over the phone), and I knew he wasn't likely to cooperate if I called him a jerk (although he was), so I treated him like a gentleman, in spite of his grumblings, so the job could get done.
Sunday, July 24, 2005
Invention or Discovery?
For example, in my first inventions, previously described on this blog, there was a square-root relationship that was measured, but never fully explained.
Sometimes the results go far beyond what is expected, so that the inventor is just as amazed as any one else. I want to tell you about an invention like that. This invention, called a Phase Meter, aims to improve the performance of the Global Positioning System (GPS) , which allows GPS users to precisely locate themselves anywhere in the world.
The GPS satellites carry atomic clocks for very precise time-keeping. They are called 'atomic' because the timing is based on the vibration of atoms, free from friction and other flaws that spoil the precision of other clocks. Atomic clocks are so accurate that scientists have been able to observe the slowing of earth's rotation, so that one year is one second longer than another. (Official time standards now have leap seconds.) Each GPS satellite has three or four atomic clocks; some are based on the vibration of cesium atoms, and some use rubidium atoms.
The timing signals of a GPS satellite are based on a 10.23 Mhz clock, that is, 10,230,000 'ticks' per second. The second, of course, is 1/60th of a minute, which is 1/60th of a hour, which is 1/24th of a day, which is based on the rotation of the earth. But the timing of an atomic clock, based on the vibration of atoms, has no natural relationship to the rotation of the earth. The output of a GPS rubidium atomic clock is about 13.401,343,936 Mhz, and 13.400,337,86 for a cesium atomic clock.
The GPS electronics needs to continually adjust its 10.23 Mhz clock, guided by the more accurate 13.40.. Mhz atomic clock output. The GPS circuits count how many cycles of the atomic clock output occur during 1.5 seconds as measured by the 10.23 Mhz clock, but that doesn't measure any fraction of a cycle left after counting whole cycles. To get the accuracy needed, the fraction of a cycle needs to be measured. That's about as awkward as trying to adjust a yardstick, marked off in inches, by using a more accurate meter-stick, marked off in centimeters, with error less that the space between the ruler marks.
The clock signals, when graphed, look like this:
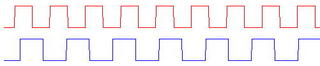 Each signal snaps up and down, between 'one' (high) and 'zero' (low), but with different time-scales. There doesn't seem to be any easy way to compare one with the other, to see if one clock is too fast or too slow, as measured by the other. Previous attempts to do this used faster clocks, which was awkward and expensive, and not accurate enough.
Each signal snaps up and down, between 'one' (high) and 'zero' (low), but with different time-scales. There doesn't seem to be any easy way to compare one with the other, to see if one clock is too fast or too slow, as measured by the other. Previous attempts to do this used faster clocks, which was awkward and expensive, and not accurate enough.One day, I wondered what would happen if one clock was 'sampled' by the other. That is, whenever the bottom clock goes 'up', we look at the top one to see if it is 1 (up) or 0 (down). Doing that for the graph above, we get the sequence 1 ? 0 1 1 0 ? 1, where ? indicates a 'close call'. So far, this sequence of 'clock samples' doesn't seem to make any sense. Is there something we can do to make some sense of this sequence of samples?
Suppose we approximate the ratio of the two clock rates (time scales) by a ratio of integers. For example, 23 cycles of the 10.23 Mhz clock are nearly equal to 36 cycles of the 13.4 Mhz clock. I thought that perhaps the following sequence might unravel the sequence of samples:
13 = the remainder when 36 is divided by 23
3 = the remainder when 36 x 2 is divided by 23
16 = the remainder when 36 x 3 is divided by 23
6 = the remainder when 36 x 4 is divided by 23
etc.
The sequence can be obtained by adding 36 to the previous number, then subtracting 23 as often as needed to reduce the value to less than 23. This process generates the following repeating sequence:
13, 3, 16, 6, 19, 9, 22, 12, 2, 15, 5, 18, 8, 21, 11, 1, 14, 4, 17, 7, 20, 10, 0...
The sequence is also a permutation, because all the integers from 0 to 22 appear exactly once each, but in a scrambled (permuted) order.
I tried the idea of using this permutation sequence to permute (scramble) the sequence of clock samples. Think of a circle labeled with the numbers 0 through 22, something like the way a wall clock is labeled with the numbers 1 through 12. We generate the permutation sequence at the same time as we generate the sequence of clock samples, and we use the permutation numbers to place the clock samples on the circle. When I first tried this, I saw a sequence of samples around the circle that looked something like this:
0000000?1111111111?0000
-- where the ? marks 'close call' samples. WOW! The sequence no longer looks random! The permutation has actually unscrambled the samples into a sensible sequence! It actually looks like one cycle of a clock signal, as illustrated here:
0000000?1111111111?0000
' ' ' ' __________
_______/ . . . . .\____
Further experiments showed that this unscrambled sequence actually gives a picture of how one clock aligns with one cycle of the other at the beginning and end of the sampling process. If one of the clocks goes faster or slower, the 'picture' shifts to the left or right.
The next step of the inventing process was to figure out a way to measure the position of the 'up' and 'down' in the 'picture' generated by the unscrambled sequence. I worked out two different methods of doing this, which led to two different patents. A fellow engineer and Christian brother, John Petzinger, helped me with the second method, so he is listed as co-inventor on the second patent.
I have illustrated the principles of the invention using the integers 23 and 36. But more accurate measurements are possible with larger integers that better approximate the clock ratio. I wrote a computer program to simulate the phase meter invention, to evaluate its performance when the clocks are compared for about one second, and this analysis predicted that the clocks could be compared with an error of only one picosecond.
"What's a picosecond?" you may ask. A picosecond is one-thousandth of a nanosecond, which is one-thousandth of a microsecond, which is one-thousandth of a millisecond, which is one-thousandth of a second. That is, a picosecond is one millionth of one millionth of a second. If a second were the distance from New York to Los Angelos, then a picosecond would be the thickness of a hair.
Going back to the analogy of comparing a yard-stick to a meter-stick, it would be like measuring the difference with an error of a hair's-breadth, even though the spacings of the 'tick'-marks on the rulers (one inch on the yard-stick and one centimeter on the meter-stick) are not nearly that small. Even the inventor is amazed.






