Invention or Discovery?

I think most people think an invention is entirely a 'bright idea' or a 'stroke of genius'; but actually, inventions are generally partly an intuitive idea and partly discovery -- at least that is what I have observed with my inventions. That is, there is a part that is understood, and a part that is not understood, at least initially. The idea has to be tried and tested to discover what happens, and if the desired result is achieved. When success is achieved, the inventor can't say "I told you so", but only "I was hoping it would work." After some experimentation and analysis, the unknown part may be understood; but sometimes it remains mysterious, even to the inventor.

For example, in my first inventions, previously described on this blog, there was a square-root relationship that was measured, but never fully explained.

Sometimes the results go far beyond what is expected, so that the inventor is just as amazed as any one else. I want to tell you about an invention like that. This invention, called a Phase Meter, aims to improve the performance of the Global Positioning System (GPS) , which allows GPS users to precisely locate themselves anywhere in the world.

The GPS satellites carry atomic clocks for very precise time-keeping. They are called 'atomic' because the timing is based on the vibration of atoms, free from friction and other flaws that spoil the precision of other clocks. Atomic clocks are so accurate that scientists have been able to observe the slowing of earth's rotation, so that one year is one second longer than another. (Official time standards now have leap seconds.) Each GPS satellite has three or four atomic clocks; some are based on the vibration of cesium atoms, and some use rubidium atoms.

The timing signals of a GPS satellite are based on a 10.23 Mhz clock, that is, 10,230,000 'ticks' per second. The second, of course, is 1/60th of a minute, which is 1/60th of a hour, which is 1/24th of a day, which is based on the rotation of the earth. But the timing of an atomic clock, based on the vibration of atoms, has no natural relationship to the rotation of the earth. The output of a GPS rubidium atomic clock is about 13.401,343,936 Mhz, and 13.400,337,86 for a cesium atomic clock.

The GPS electronics needs to continually adjust its 10.23 Mhz clock, guided by the more accurate 13.40.. Mhz atomic clock output. The GPS circuits count how many cycles of the atomic clock output occur during 1.5 seconds as measured by the 10.23 Mhz clock, but that doesn't measure any fraction of a cycle left after counting whole cycles. To get the accuracy needed, the fraction of a cycle needs to be measured. That's about as awkward as trying to adjust a yardstick, marked off in inches, by using a more accurate meter-stick, marked off in centimeters, with error less that the space between the ruler marks.

The clock signals, when graphed, look like this:

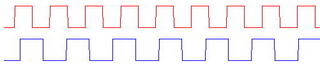Each signal snaps up and down, between 'one' (high) and 'zero' (low), but with different time-scales. There doesn't seem to be any easy way to compare one with the other, to see if one clock is too fast or too slow, as measured by the other. Previous attempts to do this used faster clocks, which was awkward and expensive, and not accurate enough.

One day, I wondered what would happen if one clock was 'sampled' by the other. That is, whenever the bottom clock goes 'up', we look at the top one to see if it is 1 (up) or 0 (down). Doing that for the graph above, we get the sequence 1 ? 0 1 1 0 ? 1, where ? indicates a 'close call'. So far, this sequence of 'clock samples' doesn't seem to make any sense. Is there something we can do to make some sense of this sequence of samples?

Suppose we approximate the ratio of the two clock rates (time scales) by a ratio of integers. For example, 23 cycles of the 10.23 Mhz clock are nearly equal to 36 cycles of the 13.4 Mhz clock. I thought that perhaps the following sequence might unravel the sequence of samples:

13 = the remainder when 36 is divided by 23
3 = the remainder when 36 x 2 is divided by 23
16 = the remainder when 36 x 3 is divided by 23
6 = the remainder when 36 x 4 is divided by 23
etc.

The sequence can be obtained by adding 36 to the previous number, then subtracting 23 as often as needed to reduce the value to less than 23. This process generates the following repeating sequence:

13, 3, 16, 6, 19, 9, 22, 12, 2, 15, 5, 18, 8, 21, 11, 1, 14, 4, 17, 7, 20, 10, 0...

The sequence is also a permutation, because all the integers from 0 to 22 appear exactly once each, but in a scrambled (permuted) order.

I tried the idea of using this permutation sequence to permute (scramble) the sequence of clock samples. Think of a circle labeled with the numbers 0 through 22, something like the way a wall clock is labeled with the numbers 1 through 12. We generate the permutation sequence at the same time as we generate the sequence of clock samples, and we use the permutation numbers to place the clock samples on the circle. When I first tried this, I saw a sequence of samples around the circle that looked something like this:

0000000?1111111111?0000

-- where the ? marks 'close call' samples. WOW! The sequence no longer looks random! The permutation has actually unscrambled the samples into a sensible sequence! It actually looks like one cycle of a clock signal, as illustrated here:

0000000?1111111111?0000
' ' ' ' __________
_______/ . . . . .\____

Further experiments showed that this unscrambled sequence actually gives a picture of how one clock aligns with one cycle of the other at the beginning and end of the sampling process. If one of the clocks goes faster or slower, the 'picture' shifts to the left or right.

The next step of the inventing process was to figure out a way to measure the position of the 'up' and 'down' in the 'picture' generated by the unscrambled sequence. I worked out two different methods of doing this, which led to two different patents. A fellow engineer and Christian brother, John Petzinger, helped me with the second method, so he is listed as co-inventor on the second patent.

I have illustrated the principles of the invention using the integers 23 and 36. But more accurate measurements are possible with larger integers that better approximate the clock ratio. I wrote a computer program to simulate the phase meter invention, to evaluate its performance when the clocks are compared for about one second, and this analysis predicted that the clocks could be compared with an error of only one picosecond.

"What's a picosecond?" you may ask. A picosecond is one-thousandth of a nanosecond, which is one-thousandth of a microsecond, which is one-thousandth of a millisecond, which is one-thousandth of a second. That is, a picosecond is one millionth of one millionth of a second. If a second were the distance from New York to Los Angelos, then a picosecond would be the thickness of a hair.

Going back to the analogy of comparing a yard-stick to a meter-stick, it would be like measuring the difference with an error of a hair's-breadth, even though the spacings of the 'tick'-marks on the rulers (one inch on the yard-stick and one centimeter on the meter-stick) are not nearly that small. Even the inventor is amazed.