Prayer in the Workplace

I've always felt that there is no area of life that is off-limits for God. So during my career as an electronics engineer, I've prayed for help with the technical stuff, not just people problems, etc. It's obvious to me that God is an engineer, too. (We're always copying his designs.) So why shouldn't he be interested in engineering matters, and know how they should be handled?

I was always taking challenges that strain my innate abilities. One area of strain is math -- I'm no mathematician, but I've had to use it, and learn it, to get the job done. Mathematicians create new mathematical knowledge, and are concerned with proofs, but not so for engineers. Engineers only use math as a tool, as needed. We are content to use unproven and approximate math -- as long as it works for us. So I've learned only a few specialized areas of math that I needed, like it or not, and only as much as needed.

God often answered my prayers for help with engineering matters, but one case stands out in my mind, so I want to tell you about it. The solution may be too complex for a general audience, but as is often the case, it is much easier to describe the problem than its solution. I think I can describe this problem in not-too-mathematical terms.

The problem involved permutations -- patterns of rearranging sequences, such as changing the sequence 1,2,3,4 to 2,4,3,1. I needed to find permutations with special properties, or else find that no such permutation existed.

Imagine that I have a cube, which has eight corners, and I have attached eight labels to the cube, one label on each corner, as follows:

The four labels on the front are red; the four at the back are green.
The four labels on the left are light; the four at the right are dark.
The four labels on the top are wide; the four at the bottom are narrow.

So every label is different. For example, there is only one wide, light red label.

So here's the problem: Can I move the labels so that I still have eight labels on the cube, one label on each corner, but arranged so that ALL of the following are true? :

Two of the red labels are on the front, and the other two are at the back.
Two of the red labels are on the left, and the other two are at the right.
Two of the red labels are on the top, and the other two are at the bottom.
All of the above should also be true for the green labels, the light labels, the dark labels, the wide labels, and the narrow labels.

Wow! That's a lot of restrictions! If you think that it is easy to find an arrangement satisfying all those restrictions, you are invited to get a cube and eight Post-It stickers and try it. But it is hard -- unless you make a computer do all the work.

So I put a computer to work trying all the permutations (changes of positions) -- and it made a list of permutations that satisfied all of the required restrictions. Problem solved.

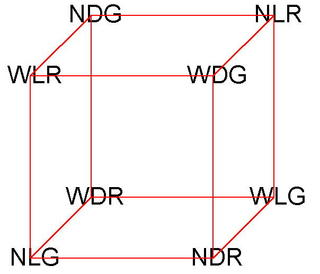Here is one solution to the problem, in case you think it is impossible. The letters stand for Narrow, Wide, Dark, Light, Red, and Green. Pick any one of these letters, and you can see that two are on top and two at bottom, two are on the left and two at right, and two are in front and two at back.

But that was just a warm-up exercise. What I really wanted to do was solve problems like the one just described, but bigger. You see, the cube has only three dimensions: front-back, left-right, and top-bottom. I wanted to solve the problem for larger numbers of dimensions.

If you have trouble visualizing more dimensions (who wouldn't?), here's an easy trick: Just add another cube and put it behind the first one. Now we have sixteen corners and sixteen labels, and another dimension which we can call FRONT-BACK, referring to the FRONT cube and BACK cube. And we can add another pair of attributes for the labels: paper and plastic. Initially, the labels on the FRONT cube are paper, and the labels on the BACK cube are plastic. Then we can define a similar problem that is twice as big, with four dimensions. And we can do something like that again to add another dimension, etc.

Each time another dimension is added, the problem gets twice as big in terms of the number of corners and labels. But in terms of difficulty, it gets much worse than twice as difficult. It's more like the sequence:

Find a button in a purse.
Find a button in a house.
Find a button in a town.
Find a button in a state.
Find a button in a country.
... You get the idea.

So in the first case, my computer found a solution in a few minutes. The next problem took a few hours. Then overnight for several nights. Then I started using my 'multi-processing' setup, where as many as 60 computers on the company network applied their 'spare time' (mostly overnight) for a week or more to solve the problem. I optimized the program to take advantage of symmetries, but I couldn't go as far as I wanted, because the work was growing too fast. I didn't have a million computers and a million years.

I needed real math, not a brute-force search. But I didn't know any math that would help. I didn't even know the language to be able to search for whatever specialized math might be applicable to such an odd problem. I was in need of prayer, and I had been praying.

I sometimes pray while driving. (If it weren't for my guardian angel, it would be as dangerous as using a cell phone.) I was driving home, pondering my growing problem and praying, and an idea came to me. Perhaps I could somehow merge two smaller permutations to make a larger one that worked (satisfied all the restrictions). After finding a bunch of permutations that work for say, five dimensions, I could try merging pairs of these and see if I can find one that works for six dimensions. But how do I merge them? And would this tactic work? This wasn't real math -- just guessing; but it might work.

I guessed at a merging function, and tried it. It didn't work all the time, but just by picking smaller permutations randomly and merging them, the computer could find larger permutations quicker than before -- very much quicker. Problems that took 60 computers several nights to solve now were solved by one computer in less than a second. And problems that would have needed a million computers and a million years were now solved by one computer in less than a minute.

I know I'm not that smart. I know God answers prayer. Even for weird math problems.